T型报价字段说明
| 第52行: | 第52行: | ||
期权的理论价值受不同的因素所影响。这些因素包括股票价格/指数水平、行权价、波动率、利率及到期日等。投资者可使用本计算器,输入不同的参数来计算期权的理论价值。本计算器使用布莱克-舒尔斯(Black-Scholes)期权定价模型进行计算,并假设行权方式为欧式。 | 期权的理论价值受不同的因素所影响。这些因素包括股票价格/指数水平、行权价、波动率、利率及到期日等。投资者可使用本计算器,输入不同的参数来计算期权的理论价值。本计算器使用布莱克-舒尔斯(Black-Scholes)期权定价模型进行计算,并假设行权方式为欧式。 | ||
| − | + | '''图中红色数标数据可在对应黄色数标位置中获取。''' | |
1、点击【期权工具】,进入期权计算器。 | 1、点击【期权工具】,进入期权计算器。 | ||
| 第66行: | 第66行: | ||
以上图为例按照以下步骤使用本计算器: | 以上图为例按照以下步骤使用本计算器: | ||
| − | + | 第1步:在上图黄色2区,选择标的物50ETF后,计算器中的“标的价”位置会自动获取该标的物的实时价格2.329元。 | |
第2步: 选择需要计算合约的行权价填入“行权价”中2.45元的合约。 | 第2步: 选择需要计算合约的行权价填入“行权价”中2.45元的合约。 | ||
| 第76行: | 第76行: | ||
第5步:“持有收益”填入无风险利率,如有分红的话减去分红。我们填入0.04。 | 第5步:“持有收益”填入无风险利率,如有分红的话减去分红。我们填入0.04。 | ||
| − | + | 第6步:选择所计算期权合约的“剩余天数”。可在报价表中的各月份标题后找到该数据。目前合约到期日均为到期月份的第四个星期三。我们填入16天。 | |
| − | + | 第7步:点击‘计算期权价值’,最终的计算结果将显示在对应的位置。计算结果,该和约的参考价值:0.0159。 | |
| − | + | 第8步:点击“计算隐含波”,结果中的隐含波数据会显示最新结果。 | |
'''温馨提示:''' | '''温馨提示:''' | ||
| − | + | 布莱克-舒尔斯(Black-Scholes)期权定价模型中使用的利率,是以连续复利计的无风险利率,无风险利率可以参考一年期国债利率、一年期Shibor利率或者一年期存贷款基准利率等。 | |
| − | + | 布莱克-舒尔斯(Black-Scholes)期权定价模型中使用的波动率,可输入投资者预期的标的证券波动率,或是通过期权价格反推出来的隐含波动率,也可以选择过去一段时间股票历史波动率作为近似参考。计算器中提供的过去一段时间的标的证券波动率,是使用过去一段时间内股票每日收盘价计算得出收益率,再求其年化标准差,截取的时间段为1个月、2个月、3个月、6个月以及1年,因此对应得出1个月、2个月、3个月、6个月以及1年的历史波动率。 | |
| − | + | 上海证券交易所目前交易的均是欧式期权,提供的期权计算器使用的是布莱克-舒尔斯(Black-Scholes)期权定价模型,由于这一模型设有以下前提条件,因此计算结果仅作为期权理论价格的参考,不作为投资者交易的标准。 | |
1、股票价格行为服从对数正态分布模式; | 1、股票价格行为服从对数正态分布模式; | ||
2015年2月9日 (一) 08:48的版本
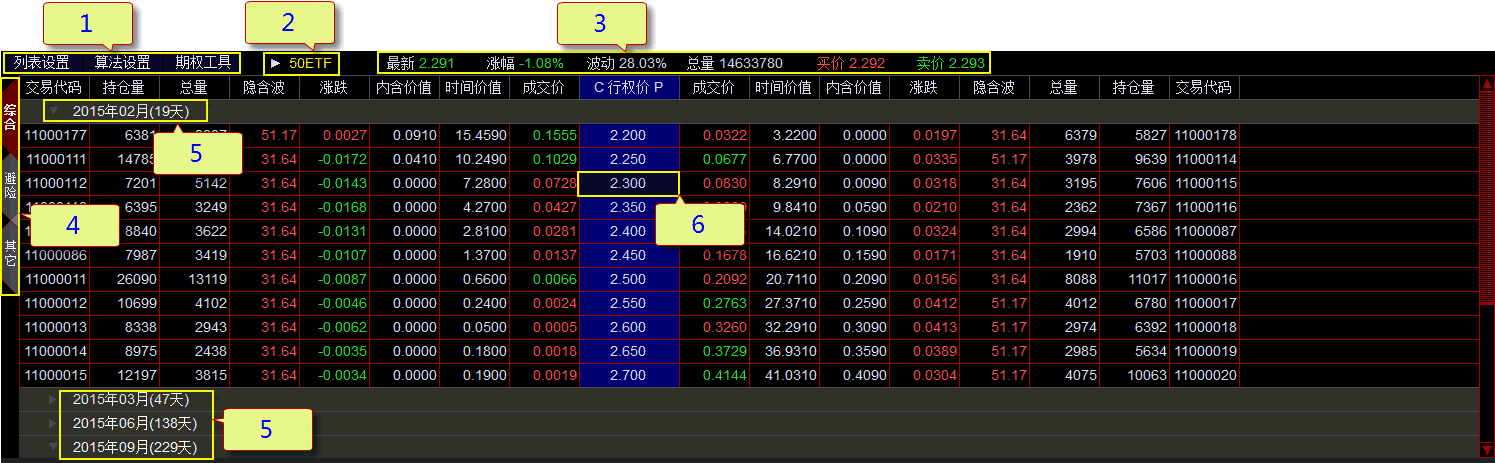
T型报价界面的特点是:归类清晰,查看方便,不容易出错。
点击【期权】-【期权T型报价】进入;
如图所示,报价窗口顶端是工具栏,下方是列表
1区说明:
表头设置(按钮):自定义表头字段,可选字段将在下面详细说明。
1. 表头可选的字段。
2. 表头已选的字段。
3. 对应切换T型报价表:1综合,2避险,3其他列表
4. 添加字段到当前列表。
5. 删除当前列表字段。
6. 选中字段在列表中左移。
7. 选中字段在列表中右移。
8. 选中,报价表将以行权价最接近标的物现价为中心,通过不同的颜色表示行权价在1倍标准差,2倍标准差和3倍标准差的合约。
9. 选中,报价表将恢复系统默认排列。
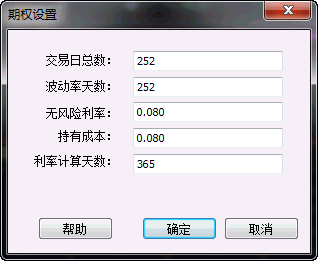
算法设置(按钮):设置定价模型的计算参数
交易日总数:用于计算年化波动率
波动率天数:用于计算标的物波动率的采样天数
无风险利率:定价模型中的 r
持有成本定价:模型中的 b
利率计算天数:用于计算定价模型中的T
期权工具(按钮):期权计算器
期权的理论价值受不同的因素所影响。这些因素包括股票价格/指数水平、行权价、波动率、利率及到期日等。投资者可使用本计算器,输入不同的参数来计算期权的理论价值。本计算器使用布莱克-舒尔斯(Black-Scholes)期权定价模型进行计算,并假设行权方式为欧式。
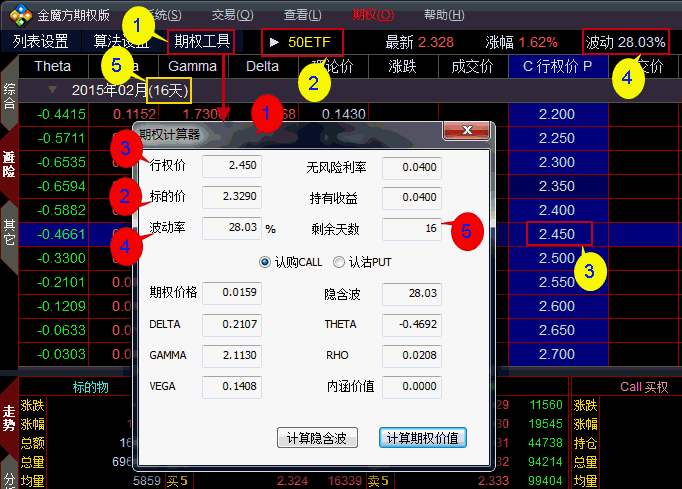
图中红色数标数据可在对应黄色数标位置中获取。
1、点击【期权工具】,进入期权计算器。
2、点击图中2点,选择标的物并获取标的物实时价格。(该数据会自动实时更新)
3、选择需计算合约的行权价。
4、标的物波动率,系统默认自动获取。
5、剩余天数。
以上图为例按照以下步骤使用本计算器:
第1步:在上图黄色2区,选择标的物50ETF后,计算器中的“标的价”位置会自动获取该标的物的实时价格2.329元。
第2步: 选择需要计算合约的行权价填入“行权价”中2.45元的合约。
第3步:在“波动率”中,您可以输入您预期的标的证券波动率。系统默认自动填充该数据28.03%。
第4步:“无风险利率”可以参考一年期国债利率、一年期Shibor利率或者一年期存贷款基准利率等,具体可登陆上证债券信息网 中国人民银行网站 或上海银行间同业拆放利率网站查询。我们填入查询到的最新数据0.04.
第5步:“持有收益”填入无风险利率,如有分红的话减去分红。我们填入0.04。
第6步:选择所计算期权合约的“剩余天数”。可在报价表中的各月份标题后找到该数据。目前合约到期日均为到期月份的第四个星期三。我们填入16天。
第7步:点击‘计算期权价值’,最终的计算结果将显示在对应的位置。计算结果,该和约的参考价值:0.0159。
第8步:点击“计算隐含波”,结果中的隐含波数据会显示最新结果。
温馨提示:
布莱克-舒尔斯(Black-Scholes)期权定价模型中使用的利率,是以连续复利计的无风险利率,无风险利率可以参考一年期国债利率、一年期Shibor利率或者一年期存贷款基准利率等。
布莱克-舒尔斯(Black-Scholes)期权定价模型中使用的波动率,可输入投资者预期的标的证券波动率,或是通过期权价格反推出来的隐含波动率,也可以选择过去一段时间股票历史波动率作为近似参考。计算器中提供的过去一段时间的标的证券波动率,是使用过去一段时间内股票每日收盘价计算得出收益率,再求其年化标准差,截取的时间段为1个月、2个月、3个月、6个月以及1年,因此对应得出1个月、2个月、3个月、6个月以及1年的历史波动率。
上海证券交易所目前交易的均是欧式期权,提供的期权计算器使用的是布莱克-舒尔斯(Black-Scholes)期权定价模型,由于这一模型设有以下前提条件,因此计算结果仅作为期权理论价格的参考,不作为投资者交易的标准。
1、股票价格行为服从对数正态分布模式;
2、在期权有效期内,无风险利率和金融资产收益变量是恒定的;
3、市场无摩擦,即不存在税收和交易成本,所有证券完全可分割;
4、金融资产在期权有效期内无红利及其它所得(该假设后被放弃);
5、该期权是欧式期权,即在期权到期前不可行权;
6、不存在无风险套利机会;
7、证券交易是持续的;
8、投资者能够以无风险利率借贷。
2区说明:
切换期权品种:通过标的物来切换报价表。选择标的物后,所有合约月份将会自动以折叠方式排列在报价表中,并在月份后显示到期时间,如图中5区。
3区说明:
信息显示区域:显示波动率和标的物的最新报价。
4区说明:
列表切换:由于字段较多,列表分成了3列,通过点击Tab切换;列表1,2,3都可以通过表头设置来定制
列表区域:列表区域列出相同标的物和相同到期日的合约,以中间的行权价从大到小排序,行权价左边是 Call 合约,右边是 Put 合约。最接近标的物最新价的合约颜色加深显示。合约中无效字段留空。
5区说明:
合约月份:选中标的物后,合约所有月份将以折叠方式排列,点击可展开或缩放。
6区说明:
最靠近标的物当前价的合约在报价表中以深色区分。